Fault Dispute Game

Table of Contents

• Overview
• Definitions
  • Virtual Machine (VM)
  • PreimageOracle
  • Execution Trace
  • Claims
  • Anchor State
  • Anchor State Registry
  • DAG
  • Subgame
  • Game Tree
  • Position
  • MAX_CLOCK_DURATION
  • CLOCK_EXTENSION
  • Freeloader Claims
• Core Game Mechanics
  • Actors
  • Moves
    • Attack
    • Defend
  • L2 Block Number Challenge
  • Step
  • Step Types
  • PreimageOracle Interaction
  • Team Dynamics
  • Game Clock
  • Resolution
    • Resolving the L2 Block Number Challenge
  • Finalization

Overview

The Fault Dispute Game (FDG) is a specific type of dispute game that verifies the validity of a root claim by iteratively bisecting over output roots and execution traces of single block state transitions down to a single instruction step. It relies on a Virtual Machine (VM) to falsify invalid claims made at a single instruction step.

Actors, i.e. Players, interact with the game by making claims that dispute other claims in the FDG. Each claim made narrows the range over the entire historical state of L2, until the source of dispute is a single state transition. Once a time limit is reached, the dispute game is resolved, based on claims made that are disputed and which aren't, to determine the winners of the game.

Definitions

Virtual Machine (VM)

This is a state transition function (STF) that takes a pre-state and computes the post-state. The VM may access data referenced during the STF and as such, it also accepts a proof of this data. Typically, the pre-state contains a commitment to the proof to verify the integrity of the data referenced.

Mathematically, we define the STF as $VM(S_i,P_i)$ where

• $S_i$ is the pre-state
• $P_i$ is an optional proof needed for the transition from $S_i$ to $S_{i+1}$.

PreimageOracle

This is a pre-image data store. It is often used by VMs to read external data during its STF. Before successfully executing a VM STF, it may be necessary to preload the PreimageOracle with pertinent data. The method for key-based retrieval of these pre-images varies according to the specific VM.

Execution Trace

An execution trace $T$ is a sequence $(S_0,S_1,S_2,...,S_n)$ where each $S_i$ is a VM state and for each $i$, $0\le i<n$, $S_{i+1}=VM(S_i,P_i)$. Every execution trace has a unique starting state, $S_0$, that's preset to a FDG implementation. We refer to this state as the ABSOLUTE_PRESTATE.

Claims

Claims assert an output root or the state of the FPVM at a given instruction. This is represented as a Hash type, a bytes32 representing either an output root or a commitment to the last VM state in a trace. A FDG is initialized with an output root that corresponds to the state of L2 at a given L2 block number, and execution trace subgames at SPLIT_DEPTH + 1 are initialized with a claim that commits to the entire execution trace between two consecutive output roots (a block n -> n+1 state transition). As we'll see later, there can be multiple claims, committing to different output roots and FPVM states in the FDG.

Anchor State

An anchor state, or anchor output root, is a previous output root that is assumed to be valid. An FDG is always initialized with an anchor state and execution is carried out between this anchor state and the claimed output root. FDG contracts pull their anchor state from the Anchor State Registry contract. The initial anchor state for a FDG is the genesis state of the L2.

Clients must currently gather L1 data for the window between the anchor state and the claimed state. In order to reduce this L1 data requirement, claims about the state of the L2 become new anchor states when dispute games resolve in their favor. FDG contracts set their anchor states at initialization time so that these updates do not impact active games.

Anchor State Registry

The Anchor State Registry is a registry that maps FDG types to their current anchor states. The Anchor State Registry is specific to Fault Dispute Game contracts and may not be applicable to other types of dispute game contracts that do not have the same concept of state that progresses over time.

DAG

A Directed Acyclic Graph $G=(V,E)$ representing the relationship between claims, where:

• $V$ is the set of nodes, each representing a claim. Formally, $V=\{C_1,C_2,...,C_n\}$, where $C_i$ is a claim.
• $E$ is the set of directed edges. An edge $(C_i,C_j)$ exists if $C_j$ is a direct dispute against $C_i$ through either an "Attack" or "Defend" move.

Subgame

A sub-game is a DAG of depth 1, where the root of the DAG is a Claim and the children are Claims that counter the root. A good mental model around this structure is that it is a fundamental dispute between two parties over a single piece of information. These subgames are chained together such that a child within a subgame is the root of its own subgame, which is visualized in the resolution section. There are two types of sub-games in the fault dispute game:

1. Output Roots
2. Execution Trace Commitments

At and above the split depth, all subgame roots correspond to output roots, or commitments to the full state of L2 at a given L2 block number. Below the split depth, subgame roots correspond to commitments to the fault proof VM's state at a given instruction step.

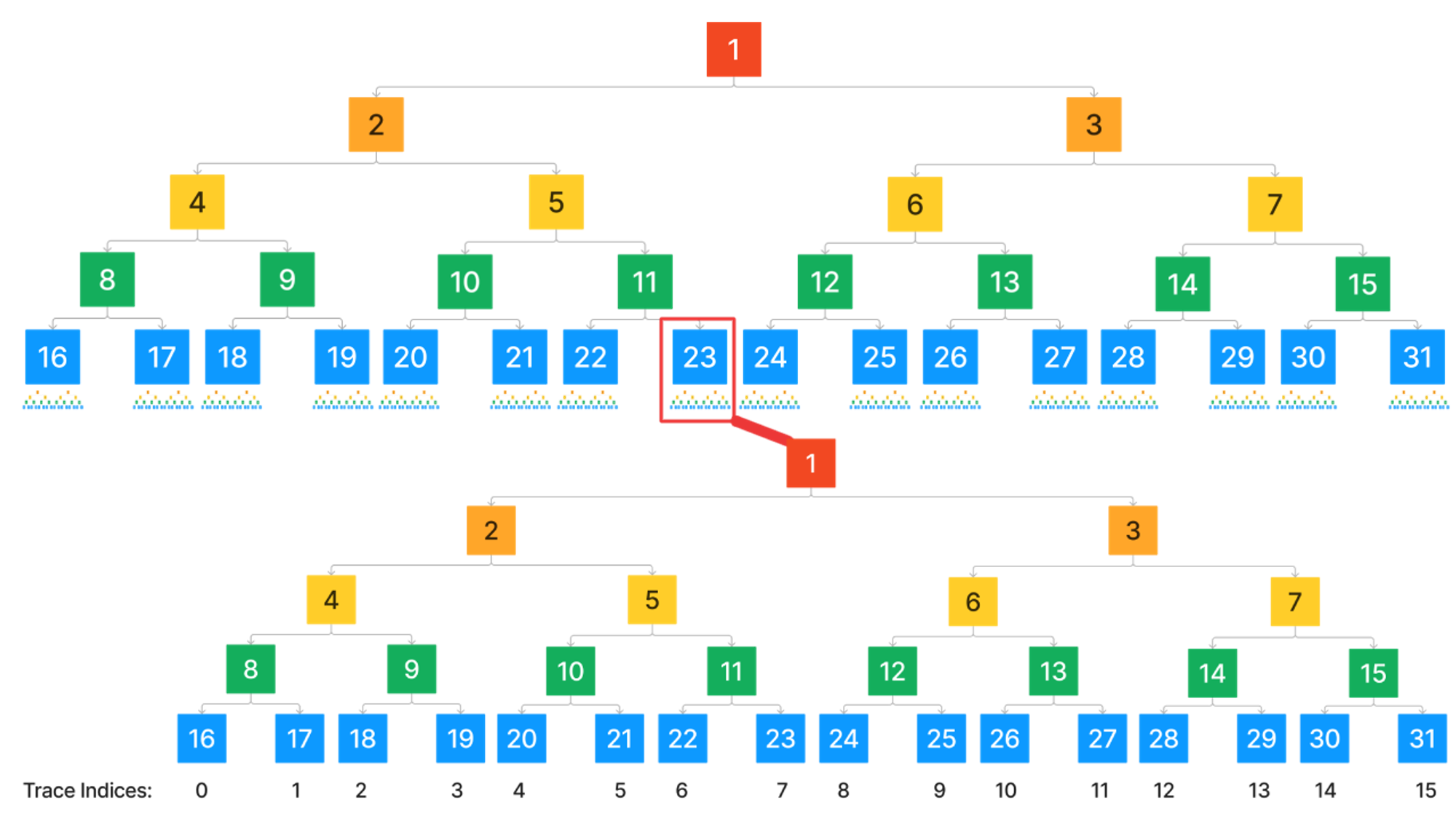
Game Tree

The Game Tree is a binary tree of positions. Every claim in the DAG references a position in the Game Tree. The Game Tree has a split depth and maximum depth, SPLIT_DEPTH and MAX_GAME_DEPTH respectively, that are both preset to an FDG implementation. The split depth defines the maximum depth at which claims about output roots can occur, and below it, execution trace bisection occurs. Thus, the Game Tree contains $2^{d+1}-1$ positions, where $d$ is the MAX_GAME_DEPTH (unless $d=0$, in which case there's only 1 position).

The full game tree, with a layer of the tree allocated to output bisection, and sub-trees after an arbitrary split depth, looks like:

Position

A position represents the location of a claim in the Game Tree. This is represented by a "generalized index" (or gindex) where the high-order bit is the level in the tree and the remaining bits is a unique bit pattern, allowing a unique identifier for each node in the tree.

The gindex of a position $n$ can be calculated as $2^{d(n)}+idx(n)$, where:

• $d(n)$ is a function returning the depth of the position in the Game Tree
• $idx(n)$ is a function returning the index of the position at its depth (starting from the left).

Positions at the deepest level of the game tree correspond to indices in the execution trace, whereas claims at the split depth represent single L2 blocks' output roots. Positions higher up the game tree also cover the deepest, right-most positions relative to the current position. We refer to this coverage as the trace index of a Position.

This means claims commit to an execution trace that terminates at the same index as their Position's trace index. That is, for a given trace index $n$, its state witness hash corresponds to the $S_n$ th state in the trace.

Note that there can be multiple positions covering the same trace index.

MAX_CLOCK_DURATION

This is an immutable, preset to a FDG implementation, representing the maximum amount of time that may accumulate on a team's chess clock.

CLOCK_EXTENSION

This is an immutable, preset to a FDG implementation, representing the flat credit that is given to a team's clock if their clock has less than CLOCK_EXTENSION seconds remaining.

Freeloader Claims

Due to the subgame resolution logic, there are certain moves which result in the correct final resolution of the game, but do not pay out bonds to the correct parties.

An example of this is as follows:

1. Alice creates a dispute game with an honest root claim.
2. Bob counters the honest root with a correct claim at the implied L2 block number.
3. Alice performs a defense move against Bob's counter, as the divergence exists later in Bob's view of the chain state.
4. Bob attacks his own claim.

Bob's attack against his own claim is a counter to a bad claim, but with the incorrect pivot direction. If left untouched, because it exists at a position further left than Alice's, he will reclaim his own bond upon resolution. Because of this, the honest challenger must always counter freeloader claims for incentive compatibility to be preserved.

Critically, freeloader claims, if left untouched, do not influence incorrect resolution of the game globally.

Core Game Mechanics

This section specifies the core game mechanics of the FDG. The full FDG mechanics includes a specification for Bonds. Readers should understand basic game mechanics before reading up on the Bond specification.

Actors

The game involves two types of participants (or Players): Challengers and Defenders. These players are grouped into separate teams, each employing distinct strategies to interact with the game. Team members share a common goal regarding the game's outcome. Players interact with the game primarily through moves.

Moves

A Move is a challenge against an existing claim and must include an alternate claim asserting a different trace. Moves can either be attacks or defenses and serve to update to DAG by adding nodes and edges targeting the disputed claim.

Moves within the fault dispute game can claim two separate values: output roots and execution trace commitments. At and above the SPLIT_DEPTH, claims correspond to output roots, while below the split depth, they correspond to execution trace commitments.

Initially, claims added to the DAG are uncontested (i.e. not countered). Once a move targets a claim, that claim is considered countered. The status of a claim — whether it's countered or not — helps determine its validity and, ultimately, the game's winner.

Attack

A logical move made when a claim is disagreed with. A claim at the relative attack position to a node, n, in the Game Tree commits to half of the trace of the n’s claim. The attack position relative to a node can be calculated by multiplying its gindex by 2.

To illustrate this, here's a Game Tree highlighting an attack on a Claim positioned at 6.

Attacking the node at 6 moves creates a new claim positioned at 12.

Defend

The logical move against a claim when you agree with both it and its parent. A defense at the relative position to a node, n, in the Game Tree commits to the first half of n + 1’s trace range.

Note that because of this, some nodes may never exist within the Game Tree. However, they're not necessary as these nodes have complimentary, valid positions with the same trace index within the tree. For example, a Position with gindex 5 has the same trace index as another Position with gindex 2. We can verify that all trace indices have valid moves within the game:

There may be multiple claims at the same position, so long as their state witness hashes are unique.

Each move adds new claims to the Game Tree at strictly increasing depth. Once a claim is at MAX_GAME_DEPTH, the only way to dispute such claims is to step.

L2 Block Number Challenge

This is a special type of action, made by the Challenger, to counter a root claim.

Given an output root preimage and its corresponding RLP-encoded L2 block header, the L2 block number can be verified. This process ensures the integrity and authenticity of an L2 block number. The procedure for this verification involves three steps: checking the output root preimage, validating the block hash preimage, and extracting the block number from the RLP-encoded header. By comparing the challenger-supplied preimages and the extracted block number against their claimed values, the consistency of the L2 block number with the one in the provided header can be confirmed, detecting any discrepancies.

Root claims made with an invalid L2 block number can be disputed through a special challenge. This challenge is validated in the FDG contract using the aforementioned procedure. However, it is crucial to note that this challenge can only be issued against the root claim, as it's the only entity making explicit claims on the L2 block number. A successful challenge effectively disputes the root claim once its subgame is resolved.

Step

At MAX_GAME_DEPTH, the position of claims correspond to indices of an execution trace. It's at this point that the FDG is able to query the VM to determine the validity of claims, by checking the states they're committing to. This is done by applying the VM's STF to the state a claim commits to. If the STF post-state does not match the claimed state, the challenge succeeds.

/// @notice Perform an instruction step via an on-chain fault proof processor.
/// @dev This function should point to a fault proof processor in order to execute
///      a step in the fault proof program on-chain. The interface of the fault proof
///      processor contract should adhere to the `IBigStepper` interface.
/// @param _claimIndex The index of the challenged claim within `claimData`.
/// @param _isAttack Whether or not the step is an attack or a defense.
/// @param _stateData The stateData of the step is the preimage of the claim at the given
///        prestate, which is at `_stateIndex` if the move is an attack and `_claimIndex` if
///        the move is a defense. If the step is an attack on the first instruction, it is
///        the absolute prestate of the fault proof VM.
/// @param _proof Proof to access memory nodes in the VM's merkle state tree.
function step(uint256 _claimIndex, bool _isAttack, bytes calldata _stateData, bytes calldata _proof) external;

Step Types

Similar to moves, there are two ways to step on a claim; attack or defend. These determine the pre-state input to the VM STF and the expected output.

• Attack Step - Challenges a claim by providing a pre-state, proving an invalid state transition. It uses the previous state in the execution trace as input and expects the disputed claim's state as output. There must exist a claim in the DAG that commits to the input.
• Defense Step - Challenges a claim by proving it was an invalid attack, thereby defending the disputed ancestor's claim. It uses the disputed claim's state as input and expects the next state in the execution trace as output. There must exist a claim in the DAG that commits to the expected output.

The FDG step handles the inputs to the VM and asserts the expected output. A step that successfully proves an invalid post-state (when attacking) or pre-state (when defending) is a successful counter against the disputed claim. Players interface with step by providing an indicator of attack and state data (including any proofs) that corresponds to the expected pre/post state (depending on whether it's an attack or defend). The FDG will assert that an existing claim commits to the state data provided by players.

PreimageOracle Interaction

Certain steps (VM state transitions) require external data to be available by the PreimageOracle. To ensure a successful state transition, players should provide this data in advance. The FDG provides the following interface to manage data loaded to the PreimageOracle:

/// @notice Posts the requested local data to the VM's `PreimageOracle`.
/// @param _ident The local identifier of the data to post.
/// @param _execLeafIdx The index of the leaf claim in an execution subgame that requires the local data for a step.
/// @param _partOffset The offset of the data to post.
function addLocalData(uint256 _ident, uint256 _execLeafIdx, uint256 _partOffset) external;

The addLocalData function loads local data into the VM's PreimageOracle. This data consists of bootstrap data for the program. There are multiple sets of local preimage keys that belong to the FaultDisputeGame contract due to the ability for players to bisect to any block $n\to n+1$ state transition since the configured anchor state, the _execLeafIdx parameter enables a search for the starting / disputed outputs to be performed such that the contract can write to and reference unique local keys in the PreimageOracle for each of these $n\to n+1$ transitions.

For global keccak256 preimages, there are two routes for players to submit:

1. Small preimages atomically.
2. Large preimages via streaming.

Global keccak256 preimages are non-context specific and can be submitted directly to the PreimageOracle via the loadKeccak256PreimagePart function, which takes the part offset as well as the full preimage. In the event that the preimage is too large to be submitted through calldata in a single block, challengers must resort to the streaming option.

Large Preimage Proposals

Large preimage proposals allow for submitters to stream in a large preimage over multiple transactions, along-side commitments to the intermediate state of the keccak256 function after absorbing/permuting the $1088$ bit block. This data is progressively merkleized on-chain as it is streamed in, with each leaf constructed as follows:

/// @notice Returns a leaf hash to add to a preimage proposal merkle tree.
/// @param input A single 136 byte chunk of the input.
/// @param blockIndex The index of the block that `input` corresponds to in the full preimage's absorption.
/// @param stateCommitment The hash of the full 5x5 state matrix *after* absorbing and permuting `input`.
function hashLeaf(
    bytes memory input,
    uint256 blockIndex,
    bytes32 stateCommitment
) internal view returns (bytes32 leaf) {
    require(input.length == 136, "input must be exactly the size of the keccak256 rate");

    leaf = keccak256(abi.encodePacked(input, blockIndex, stateCommitment));
}

Once the full preimage and all intermediate state commitments have been posted, the large preimage proposal enters a challenge period. During this time, a challenger can reconstruct the merkle tree that was progressively built on-chain locally by scanning the block bodies that contain the proposer's leaf preimages. If they detect that a commitment to the intermediate state of the hash function is incorrect at any step, they may perform a single-step dispute for the proposal in the PreimageOracle. This involves:

1. Creating a merkle proof for the agreed upon prestate leaf (not necessary if the invalid leaf is the first one, the setup state of the matrix is constant.) within the proposal's merkle root.
2. Creating a merkle proof for the disputed post state leaf within the proposal's merkle root.
3. Computing the state matrix at the agreed upon prestate (not necessary if the invalid leaf is the first one, the setup state of the matrix is constant.)

The challenger then submits this data to the PreimageOracle, where the post state leaf's claimed input is absorbed into the pre state leaf's state matrix and the SHA3 permutation is executed on-chain. After that, the resulting state matrix is hashed and compared with the proposer's claim in the post state leaf. If the hash does not match, the proposal is marked as challenged, and it may not be finalized. If, after the challenge period is concluded, a proposal has no challenges, it may be finalized and the preimage part may be placed into the authorized mappings for the FPVM to read.

Team Dynamics

Challengers seek to dispute the root claim, while Defenders aim to support it. Both types of actors will move accordingly to support their team. For Challengers, this means attacking the root claim and disputing claims positioned at even depths in the Game Tree. Defenders do the opposite by disputing claims positioned at odd depths.

Players on either team are motivated to support the actions of their teammates. This involves countering disputes against claims made by their team (assuming these claims are honest). Uncontested claims are likely to result in a loss, as explained later under Resolution.

Game Clock

Every claim in the game has a Clock. A claim inherits the clock of its grandparent claim in the DAG (and so on). Akin to a chess clock, it keeps track of the total time each team takes to make moves, preventing delays. Making a move resumes the clock for the disputed claim and pauses it for the newly added one.

If a move is performed, where the potential grandchild's clock has less time than CLOCK_EXTENSION seconds remaining, the potential grandchild's clock is granted exactly CLOCK_EXTENSION seconds remaining. This is to combat the situation where a challenger must inherit a malicious party's clock when countering a freeloader claim, in order to preserve incentive compatibility for the honest party. As the extension only applies to the potential grandchild's clock, the max possible extension for the game is bounded, and scales with the MAX_GAME_DEPTH.

If the potential grandchild is an execution trace bisection root claim and their clock has less than CLOCK_EXTENSION seconds remaining, exactly CLOCK_EXTENSION * 2 seconds are allocated for the potential grandchild. This extra time is alloted to allow for completion of the off-chain FPVM run to generate the initial instruction trace.

A move against a particular claim is no longer possible once the parent of the disputed claim's Clock has accumulated MAX_CLOCK_DURATION seconds. By which point, the claim's clock has expired.

Resolution

Resolving the FDG determines which team won the game. To do this, we use the internal sub game structure. Each claim within the game is the root of its own sub game. These subgames are modeled as nested DAGs, each with a max depth of 1. In order for a claim to be considered countered, only one of its children must be uncountered. Subgames can also not be resolved until all of their children, which are subgames themselves, have been resolved and the potential opponent's chess clock has run out. To determine if the potential opponent's chess clock has ran out, and therefore no more moves against the subgame are possible, the duration elapsed on the subgame root's parent clock is added to the difference between the current time and the timestamp of the subgame root's creation. Because each claim is the root of its own sub-game, truth percolates upwards towards the root claim by resolving each individual sub-game bottom-up.

In a game like the one below, we can resolve up from the deepest subgames. Here, we'd resolve b0 to uncountered and a0 to countered by walking up from their deepest children, and once all children of the root game are recursively resolved, we can resolve the root to countered due to b0 remaining uncountered.

https://github.com/ethereum-optimism/optimism/assets/8406232/d2b708a0-539e-439d-96bd-c2f66f3a45f8

Another example is this game, which has a slightly different structure. Here, the root claim will also be countered due to b0 remaining uncountered.

Given these rules, players are motivated to move quickly to challenge all dishonest claims. Each move bisects the historical state of L2 and eventually, MAX_GAME_DEPTH is reached where disputes can be settled conclusively. Dishonest players are disincentivized to participate, via backwards induction, as an invalid claim won't remain uncontested. Further incentives can be added to the game by requiring claims to be bonded, while rewarding game winners using the bonds of dishonest claims.

Resolving the L2 Block Number Challenge

The resolution of an L2 block number challenge occurs in the same manner as subgame resolution, with one caveat; the L2 block number challenger, if it exist, must be the winner of a root subgame. Thus, no moves against the root, including uncontested ones, can win a root subgame that has an L2 block number challenge.

Finalization

Once the game is resolved, if the claim is shown to be valid, the FDG reports its state to the Anchor State Registry. The Anchor State Registry verifies that the request to update an anchor state comes from a FDG contract created by the Dispute Game Factory contract, confirms that the game resolved in favor of the defender, and confirms that the updated state would be newer than the current anchor state (based on the result of FaultDisputeGame.l2BlockNumber()). If these conditions are true, the Anchor State Registry updates the anchor state for the given game type.

Note that the dependency of the Anchor State Registry on the l2BlockNumber() function means that the registry may not be applicable to dispute game types that do not have a similar sense of progressing state over time. Currently, the Anchor State Registry is therefore assumed to be specific to the Fault Dispute Game contract and not to other dispute game types.